THEORY OF HEAT

PREFACE

The aim of this book is to exhibit the scientific connexion of the various steps by which our knowledge of the phenomena of heat has been extended. The first of these steps is the invention of the thermometer, by which the registration and comparison of temperatures is rendered possible. The second step is the measurement of quantities of heat, or Calorimetry. The whole science of heat is founded on Thermometry and Calorimetry, and when these operations are understood we may proceed to the third step, which is the investigation of those relations between the thermal and the mechanical properties of substances which form the subject of Thermodynamics. The whole of this part of the subject depends on the consideration of the Intrinsic Energy of a system of bodies, as depending on the temperature and physical state, as well as the form, motion, and relative position of these bodies. Of this energy, however, only a part is available for the purpose of producing mechanical work, and though the energy itself is indestructible, the available part is liable to diminution by the action of certain natural processes, such as conduction and radiation of heat, friction, and viscosity. These processes, by which energy is rendered unavailable as a source of work, are classed together under the name of the Dissipation of Energy, and form the subjects of the next division of the book. The last chapter is devoted to the explanation of various phenomena by means of the hypothesis that bodies consist of molecules, the motion of which constitutes the heat of those bodies.

In order to bring the treatment of these subjects within the limits of this text-book, it has been found necessary to omit everything which is not an essential part of the intellectual process by which the doctrines of heat have been developed, or which does not materially assist the student in forming his own judgment on these doctrines.

For this reason, no account is given of several very important experiments, and many illustrations of the theory of heat by means of natural phenomena are omitted. The student, however, will find this part of the subject treated at greater length in several excellent works on the same subject which have lately appeared.

A full account of the most important experiments on the effects of heat will be found in Dixon’s ‘Treatise on Heat’ (Hodges & Smith, 1849).

Professor Balfour Stewart’s treatise contains all that is necessary to be known in order to make experiments on heat. The student may be also referred to Deschanel’s ‘Natural Philosophy,’ Part II., translated by Professor Everett, who has added a chapter on Thermodynamics; to Professor Rankine’s work on the Steam Engine, in which he will find the first systematic treatise on thermodynamics; to Professor Tait’s ‘ Thermodynamics,’ which contains an historical sketch of the subject, as well as the mathematical investigations; and to Professor Tyndall’s work on ‘ Heat as a Mode of Motion,’ in which the doctrines of the science are forcibly impressed on the mind by well-chosen illustrative experiments. The original memoirs of Professor Clausius, one of the founders of the modern science of Thermodynamics, have been edited in English by Professor Hirst.

 

A TREATISE ON HEAT

CHAPTER I INTRODUCTION.

The distinction between hot bodies and cold ones is familiar to all, and is associated in our minds with the difference of the sensations which we experience in touching various substances, according as they are hot or cold. The intensity of these sensations is susceptible of degrees, so that we may estimate one body to be hotter or colder than another by the touch. The words hot, warm, cool, cold, are associated in our minds with a series of sensations which we suppose to indicate a corresponding series of states of an object with respect to heat.

We use these words, therefore, as the names of these states of the object, or, in scientific language, they are the names of Temperatures, the word hot indicating a high temperature, cold a low temperature, and the intermediate terms intermediate temperatures, while the word temperature itself is a general term intended to apply to any one of these states of the object

Since the state of a body may vary continuously from cold to hot, we must admit the existence of an indefinite number of intermediate states, which we call intermediate temperatures. We may give names to any number of particular degrees of temperature, and express any other temperature by its relative place among these degrees.

The temperature of a body, therefore, is a quantity which indicates how hot or how cold the body is.

When we say that the temperature of one body is higher or lower than that of another, we mean that the first body is hotter or colder than the second, but we also imply that we refer the state of both bodies to a certain scale of temperatures. By the use, therefore, of the word temperature, we fix in our minds the conviction that it is possible, not only to feel, but to measure, how hot a body is.

Words of this kind, which express the same things as the words of primitive language, but express them in a way susceptible of accurate numerical statement, are called scientific[note]’Scientifick, adj. Producing demonstrative knowledge.’ —Johnson’s Dict.[/note] terms, because they contribute to the growth of science.

We might suppose that a person who has carefully cultivated his senses would be able by simply touching an object to assign its place in a scale of temperatures, but it is found by experiment that the estimate formed of temperature by the touch depends upon a great variety of circumstances, some of these relating to the texture or consistency of the object, and some to the temperature of the hand or the state of health of the person who makes the estimate.

For instance, if the temperature of a piece of wood were the same as that of a piece of iron, and much higher than that of the hand, we should estimate the iron to be hotter than the wood, because it parts with its heat more readily to the hand, whereas if their temperatures were equal, and much lower than that of the hand, we should estimate the iron to be colder than the wood.

There is another common experiment, in which we place one hand in hot water and the other in cold for a sufficient time. If we then dip both hands in the same basin of lukewarm water alternately, or even at once, it will appear cold to the warmed hand and hot to the cooled hand.

In fact, our sensations of every kind depend upon so many variable conditions, that for all scientific purposes we prefer to form our estimate of the state of bodies from their observed action on some apparatus whose conditions are more simple and less variable than those of our own senses.

The properties of most substances vary when their temperature varies. Some of these vacations are abrupt, and serve to indicate particular temperatures as points of reference; others are continuous, and serve to measure other temperatures by comparison with the temperatures of reference.

For instance, the temperature at which ice melts is found to be always the same under ordinary circumstances, though, as we shall see, it is slightly altered by change of pressure. The temperature of steam which issues from boiling water is also constant when the pressure is constant.

These two phenomena therefore—the melting of ice and the beiling of water—indicate in a visible manner two temperatures which we may use as points of reference, the position of which depends on the properties of water and not on the conditions of our senses.

Other changes of state which take place at temperatures more or less definite, such as the melting of wax or of lead, and the boiling of liquids of definite composition, are occasionally used to indicate when these temperatures are attained, but the melting of ice and the boiling of pure water at a standard pressure remain the most important temperatures of reference in modern science.

These phenomena of change of state serve to indicate only a certain number of particular temperatures. In order to measure temperatures in general, we must avail ourselves of some property of a substance which alters continuously with the temperature.

The volume of most substances increases continuously as the temperature rises, the pressure remaining constant There are exceptions to this rule, and the dilatations of different substances are not in general in the same proportion; but any substance in which an increase of temperature, however small, produces an increase of volume may be used to indicate changes of temperature.

For instance, mercury and glass both expand when heated, but the dilatation of mercury is greater than that of glass. Hence if a cold glass vessel be filled with cold mercury, and if the vessel and the mercury in it are then equally heated, the glass vessel will expand, but the mercury will expand more, so that the vessel will no longer contain the mercury. If the vessel be provided with a long neck, the mercury forced out of the vessel will rise in the neck, and if the neck is a narrow tube finely graduated, the amount of mercury forced out of the vessel may be accurately measured.

This is the principle of the common mercurial thermometer, the construction of which will be afterwards more minutely, described. At present we consider it simply as an instrument the indications of which vary when the temperature varies, but are always the same when the temperature of the instrument is the same.

The dilatation of other liquids, as well as that of solids and of gases, may be used for thermometric purposes, and the thermo-electric properties of metals, and the variation of their electric resistance with temperature, are also employed in researches on heat. We must first, however, study the theory of temperature in itself before we examine the properties of different substances as related to temperature, and for this purpose we shall use the particular mercurial thermometer just described.

The Mercurial Thermometer.

This thermometer consists of a glass tube terminating in a bulb, the bulb and part of the tube being filled with mercury, and the rest of the tube being empty. We shall suppose the tube to be graduated in any manner so that the height of the mercury in the tube may be observed and recorded. We shall not, however, assume either that the tube is of uniform section or that the degrees are of equal size, so that the scale of this primitive thermometer must be regarded as completely arbitrary. By means of our thermometer we can ascertain whether one temperature is higher or lower than another, or equal to it, but we cannot assert that the difference between two temperatures, a and b, is greater or less than the difference between two other temperatures, c and d.

We shall suppose that in every observation the temperature of the mercury and the glass is equal and uniform over the whole thermometer. The reading of the scale will then depend on the temperature of the thermometer, and, since we have not yet established any more perfect thermometric scale, we shall call this reading provisionally ‘the temperature by the arbitrary scale of the thermometer.’

The reading of a thermometer indicates primarily its own temperature, but if we bring the thermometer into intimate contact with another substance, as for instance if we plunge it into a liquid for a sufficient time, we find that the reading of the thermometer becomes higher or lower according as the liquid is hotter or colder than the thermometer, and that if we leave the thermometer in contact with the substance for a sufficient time the reading becomes stationary. Let us call this ultimate reading ‘the temperature of the substance.’ We shall find as we go on that we have a right to do so.

Let us now take a vessel of water which we shall suppose to be at the temperature of the air, so that if left to itself it would remain at the same temperature. Take another smaller vessel of thin sheet copper or tin plate, and fill it with water, oil, or any other liquid, and immerse it in the larger vessel of water for a certain time. Then, if by means of our thermometer we register the temperatures of the liquids in the two vessels before and after the immersion of the copper vessel, we find that if they are originally at the same temperature the temperature of both remains the same, but that if one is at a higher temperature than the other, that which has the higher temperature becomes colder and that which has the lower temperature becomes hotter, so that if they continue in contact for a sufficient time they arrive at last at the same temperature, after which no change of tem-perature takes place.

The loss of temperature by the hot body is not in general
equal to the gain of temperature by the cold body, but it is manifest that the two simultaneous phenomena are due to one cause, and this cause may be described as the passage of Heat from the hot body to the cold one.

As this is the first time we have used the word Heat, let us examine what we mean by it.

We find the cooling of a hot body and the heating of a cold body happening simultaneously as parts of the same phenomenon, and we describe this phenomenon as the passage of heat from the hot body to the cold one. Heat, then, is something which may be transferred from one body to another, so as to diminish the quantity of heat in the first and increase that in the second by the same amount. When heat is communicated to a body, the temperature of the body is generally increased, but sometimes other effects are produced, such as change of state. When heat leaves a body, there is either a fall of temperature or a change of state. If no heat enters or leaves a body, and if no changes of state or mechanical actions take place in the body, the temperature of the body will remain constant.

Heat, therefore, may pass out of one body into another just as water may be poured from one vessel into another, and it may be retained in a body for any time, just as water may be kept in a vessel. We have therefore a right to speak of heat as of a measurable quantity, and to treat it mathematically like other measurable quantities so long as it continues to exist as heat. We shall find, however, that we have no right to treat heat as a substance, for it may be transformed into something which is not heat, and is certainly not a substance at all, namely, mechanical work.

We must remember, therefore, that though we admit heat to the title of a measurable quantity, we must not give it rank as a substance, but must hold our minds in suspense till we have further evidence as to the nature of heat.

Such evidence is furnished by experiments on friction, in which mechanical work, instead of being transmitted from one part of a machine to another, is apparently lost, while at the same time, and in the same place, heat is generated, the amount of heat being in an exact proportion to the amount of work lost. We have, therefore, reason to believe that heat is of the same nature as mechanical work, that is, it is one of the forms of Energy.

In the eighteenth century, when many new facts were being discovered relating to the action of heat on bodies, and when at the same time great progress was being made in the knowledge of the chemical action of substances, the word Caloric was introduced to signify heat as a measurable quantity. So long as the word denoted nothing more than this, it might be usefully employed, but the form of the word accommodated itself to the tendency of the chemists of that time to seek for new ‘imponderable substances,’ so that the word caloric came to connote[note]’A connotative term is one which denotes a subject and implies an attribute.’—Mill’s Logic, book i. chap. ii. § 5.[/note] not merely heat, but heat as an indestructible imponderable fluid, insinuating itself into the pores of bodies, dilating and dissolving them, and ultimately vaporising them, combining with bodies in definite quantities, and so becoming latent, and reappearing when these bodies alter their condition. In fact, the word caloric, when once introduced, soon came to imply the recognised existence of something material, though probably of a more subtle nature than the then newly discovered gases. Caloric resembled these gases in being invisible and in its property of becoming fixed in solid bodies. It differed from them because its weight could not be detected by the finest balances, but there was no doubt in the minds of many eminent men that caloric was a fluid pervading all bodies, probably the cause of all repulsion, and possibly even of the extension of bodies in space.

Since ideas of this kind have always been connected with the word caloric, and the word itself has been in no slight degree the means of embodying and propagating these ideas, and since all these ideas are now known to be false, we shall avoid as much as possible the use of the word caloric in treating of heat. We shall find it useful, however, when we wish to refer to the erroneous theory which supposes heat to be a substance, to call it the ‘Caloric Theory of Heat.’

The word heat, though a primitive word and not a scientific term, will be found sufficiently free from ambiguity when we use it to express a measurable quantity, because it will be associated with words expressive of quantity, indicating how much heat we are speaking of.

We have nothing to do with the word heat as an abstract term signifying the property of hot things, and when we might say a certain heat, as the heat of new milk, we shall always use the more scientific word temperature, and speak of the temperature of new milk.

We shall never use the word heat to denote the sensation of heat. In fact, it is never so used in ordinary language, which has no names for sensations, unless when the sensation itself is of more importance to us than its physical cause, as in the case of pain, &c[note]직지 주: an abbreviation of etc.[/note]. The only name we have for this sensation is ‘the sensation of heat.’

When we require an adjective to denote that a phenomenon is related to heat we shall call it a thermal phenomenon, as, for instance, we shall speak of the thermal conductivity of a substance or of thermal radiation to distinguish the conduction and radiation of heat from the conduction of electricity or the radiation of light. The science of heat has been called (by Dr. Whewell and others) Thermotics, and the theory of heat as a form of energy is called Thermodynamics. In the same way the theory of the equilibrium of heat might be called Thermostatics, and that of the motion of heat Thermokinematics.

The instrument by which the temperature of bodies is registered is called a Thermometer or measurer of warmth, and the method of constructing and using thermometers may be called Thermometry.

The instrument by which quantities of heat are measured is called a Calorimeter, probably because it was invented at a time when heat was called Caloric. The name, however, is now well established, and is a convenient one, as its form is sufficiently distinct from that of the word Thermometer. The method of measuring heat may be called Calorimetry.

A certain quantity of heat, with which all other quantities are compared, is called a Thermal Unit. This is the quantity of heat required to produce a particular effect, such as to melt a pound of ice, or to raise a pound of water from one defined temperature to another defined temperature. A particular thermal unit has been called by some authors a Calorie.

We have now obtained two of the fundamental ideas of the science of heat—the idea of temperature, or the property of a body considered with reference to its power of heating other bodies; and the idea of heat as a measurable quantity, which may be transferred from hotter bodies to colder ones. We shall consider the further development of these ideas in the chapters on Thermometry and Calorimetry, but we must first direct our attention to the process by which heat is transferred from one body to another.

This process is called the Diffusion of Heat. The diffusion of heat invariably transfers heat from a hotter body to a colder one, so as to cool the hotter body and warm the colder body. This process would go on till all bodies were brought to the same temperature if it were not for certain other processes by which the temperatures of bodies are changed independently of any exchange of heat with other bodies, as, for instance, when combustion or any other chemical process takes place, or when any change occurs in the form, structure, or physical state of the body.

The changes of temperature of a body arising from other causes than the transfer of heat from other bodies will be considered when we come to describe the different physical states of bodies. We are at present concerned only with the passage of heat into the body or out of it, and this always takes place by diffusion, and is always from a hotter to a colder body.

Three processes of diffusion of heat are commonly recognised—Conduction, Convection, and Radiation.

Conduction[note]직지 주: 전도傳道 – 열이 물체에서 온도가 높은 한 부분에서 점차 온도가 낮은 다른 부분으로 옮아 가는 현상.[/note] is the flow of heat through an unequally heated body from places of higher to places of lower temperature.

Convection[note]직지 주: 대류對流 – 열이 물질의 운동에 의하여 운반되는 현상.[/note] is the motion of the hot body itself carrying its heat with it. If by this motion it is brought near bodies colder than itself it will warm them faster than if it had not been moved nearer to them. The term convection is applied to those processes by which the diffusion of heat is rendered more rapid by the motion of the hot substance from one place to another, though the ultimate transfer of heat may still take place by conduction.

In Radiation[note]직지 주: 복사輻射 – 물체로부터 열이 사방으로 방출됨.[/note], the hotter body loses heat, and the colder body receives heat by means of a process occurring in some intervening medium which does not itself become thereby hot.

In each of these three processes of diffusion of heat the temperatures of the bodies between which the process takes place tend to become equal. We shall not at present discuss the convection of heat, because it is not a purely thermal phenomenon, since it depends on a hot substance being carried from one place to another, either by human effort, as when a hot iron is taken out of the fire and put into the tea-urn, or by some natural property of the heated substance, as when water, heated by contact with the bottom of a kettle placed on the fire, expands as it becomes warmed, and forms an ascending current, making way for colder and therefore denser water to descend and take its place. In every such case of convection the ultimate and only direct transfer of heat is due to conduction, and the only effect of the motion of the hot substance is to bring the unequally heated portions nearer to each other, so as to facilitate the exchange of heat. We shall accept the conduction of heat as a fact, without at present attempting to form any theory of the details of the process by which it takes place. We do not even assert that in the diffusion of heat by conduction the transfer of heat is entirely from the hotter to the colder body. All that we assert is, that the amount of heat transferred from the hotter to the colder body is invariably greater than the amount, if any, transferred from the colder to the hotter.

ON CONDUCTION.

In the experiments which we have described, heat passes from one body into another through an intervening substance, as from a vessel of water through the glass bulb of a thermometer into the mercury inside the bulb.

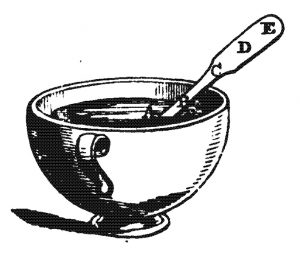
This process, by which heat passes from hotter to colder parts of a body, is called the conduction of heat. When heat is passing through a body by conduction, the temperature of the body must be greater in the parts from which the heat comes than in those to which it tends, and the quantity of heat which passes through any thin layer of the substance depends on the difference of the temperatures of the opposite sides of the layer. For instance, if we put a silver spoon into a cup of hot tea, the part of the spoon in the tea soon becomes heated, while the part just out of the tea is comparatively cool. On account of this inequality of temperature, heat immediately begins to flow along the metal from A to B. The heat first warms B a little, and so makes B warmer than C, and then the heat flows on from B to C, and in this way the very end of the spoon will in course of time become warm to the touch. The essential requisite to the conduction of heat is, that in every part of its course the heat must pass from hotter to colder parts of the body. No heat can be conducted as far as E till A has been made hotter than B, B than C, C than D, and D than E. To do this requires a certain amount of heat to be expended in warming in succession all these intermediate parts of the spoon, so that for some time after the spoon is placed in the cup no alteration of temperature can be perceived at the end of the spoon.

Hence we may define conduction as the passage of heat through a body depending on inequality of temperature in adjacent parts of the body.

When any part of a body is heated by conduction, the parts of the body through which the heat comes to it must be hotter than itself, and the parts higher up the stream of heat still hotter.

If we now try the experiment of the spoon in the teacup with a German silver spoon along with the silver one, we shall find that the end of the silver spoon becomes hot long before that of the German silver one; and if we also put in a bone or horn spoon, we shall not be able to perceive any warmth at the end of it, however long we wait.

This shows that silver conducts heat quicker than German silver, and German silver quicker than bone or horn. The reason why the end of the spoon never gets as hot as the tea is, that the intermediate parts of the spoon are cooling, partly by giving their heat to the air in contact with them, and partly by radiation out into space.

To show that the first effect of heat on the thermometer is to warm the material of which the bulb is composed, and that the heat cannot reach the fluid inside till the bulb has been warmed, take a thermometer with a large bulb, watch the fluid in the tube, and dash a little hot water over the bulb. The fluid will fall in the tube before it begins to rise, showing that the bulb began to expand before the fluid expanded.

ON RADIATION.

On a calm day in winter we feel the sun’s rays warm even when water is freezing and ice is hard and dry.

If we make use of a thermometer, we find that if the sun’s rays fall on it, it indicates a temperature far above freezing, while the air immediately surrounding the bulb is at a temperature below freezing. The heat, therefore, which we feel, and to which the thermometer also responds, is not conveyed to it by conduction through the air, for the air is cold, and a cold body cannot make a body warmer than itself by conduction. The mode in which the heat reaches the body which it warms, without warming the air through which it passes, is called radiation. Substances which admit of radiation taking place through them are called Diathermanous[note]직지 주: 투열성透熱性 – 적외선을 통과시키는 성질)[/note]. Those which do not allow heat to pass through them without becoming themselves hot are called Athermanous[note]직지 주: 불투열성不透熱性[/note]. That which passes through the medium during this process is generally called Radiant Heat, though as long as it is radiant it possesses none of the properties which distinguish heat from other forms of energy, since the temperature of the body through which it passes, and the other physical properties of the body, are in no way affected by the passage of the radiation, provided the body is perfectly diathermanous. If the body is not perfectly diathermanous it stops more or less of the radiation, and becomes heated itself, instead of transmitting the whole radiation to bodies beyond it.

The distinguishing characteristic of radiant heat is, that it travels in rays like light, whence the name radiant. These rays have all the physical properties of rays of light, and are capable of reflexion[note]직지 주: 반사[/note], refraction[note]직지 주: 굴절[/note], interference[note]직지 주: 간섭[/note], and polarisation[note]직지 주: 편광[/note]. They may be divided into different kinds by the prism, as light is divided into its component colours, and some of the heat-rays are identical with the rays of light, while other kinds of heat-rays make no impression on our eyes. For instance, if we take a glass convex lens, and place it in the sun’s rays, a body placed at the focus where a small image of the sun is formed will be intensely heated, while the lens itself and the air through which the rays pass remain quite cold. If we allow the rays before they reach the focus to fall on the surface of water, so that the rays meet in a focus in the interior of the water, then if the water is quite clear at the focus it will remain tranquil, but if we make the focus fall upon a mote in the water, the rays will be stopped, the mote will be heated and will cause the water next it to expand, and so an upward current will be produced, and the mote will begin to rise in the water. This shows that it is only when the radiation is stopped that it has any effect in heating what it falls on.

By means of any regular concave piece of metal, such as the scale of a balance, pressed when hot against a clear sheet of ice, first on one side and then on the other, it is easy to make a lens of ice which may be used on a sunny day as a burning glass; but this experiment, which was formerly in great repute, is far inferior in interest to one invented by Professor Tyndall, in which the heat, instead of being concentrated by ice, is concentrated in ice. Take a clear block of ice and make a flat surface on it, parallel to the original surface of the lake, or to the layers of bubbles generally found in large blocks; then let the converging rays of the sun from an ordinary burning glass fall on this surface, and come to a focus within the ice. The ice, not being perfectly diathermanous, will be warmed by the rays, but much more at the focus than anywhere else. Thus the ice will begin to melt at the focus in the interior of its substance, and, as it does so, the portions which melt first are regularly formed crystals, and so we see in the path of the beam a number of six-rayed stars[note]직지 주: 이 실험에 대해서는 http://www.rigb.org/our-history/bragg-film-archive/crystallography/tyndalls-ice-flowers 참조.[/note], which are hollows cut out of the ice and containing water. This water, however, does not quite fill them, because the water is of less bulk than the ice of which it was made, so that parts of the stars are empty.

Experiments on the heating effects of radiation show that not only the sun but all hot bodies emit radiation. When the body is hot enough, its radiations become visible, and the body is said to be red hot. When it is still hotter it sends forth not only red rays, but rays of every colour, and it is then said to be white hot. When a body is too cold to shine visibly, it still shines with invisible heating rays, which can be perceived by a sufficiently delicate thermometer, and it does not appear that any body can be so cold as not to send forth radiations. The reason why all bodies do not appear to shine is, that our eyes are sensitive only to particular kinds of rays, and we only see by means of rays of these kinds, coming from some very hot body, either directly or after reflexion or scattering at the surface of other bodies.

We shall see that the phrases radiation of heat and radiant heat are not quite scientifically correct, and must be used with caution. Heat is certainly communicated from one body to another by a process which we call radiation, which takes place in the region between the two bodies. We have no right, however, to speak of this process of radiation as heat. We have defined heat as it exists in hot bodies, and we have seen that all heat is of the same kind. But the radiation between bodies differs from heat as we have defined it—1st, in not making the body hot through which it passes; 2nd, in being of many different kinds. Hence we shall generally speak of radiation, and when we speak of radiant heat we do not mean to imply the existence of a new kind of heat, but to consider radiation in its thermal aspect.

 

ON THE DIFFERENT PHYSICAL STATES OF BODIES.

Bodies are found to behave in different ways under the action of forces. If we cause a longitudinal pressure to act on a body in one direction by means of a pair of pincers or a vice, the body being free to move in all other directions, we find that if the body is a piece of cold iron there is very litlle effect produced, unless the pressure be very great; if the body is a piece of india-rubber, it is compressed in the direction of its length and bulges out at the sides, but it soon comes into a state of equilibrium, in which it continues to support the pressure; but if we substitute water for the india-rubber we cannot perform the experiment, for the water flows away laterally, and the jaws of the pincers come together without having exerted any appreciable pressure.

Bodies which can sustain a longitudinal pressure, however small that pressure may be, without being supported by a lateral pressure, are called solid bodies. Those which cannot do so are called fluids. We shall see that in a fluid at rest the pressure at any point must be equal in all directions, and this pressure is called the pressure of the fluid.

There are two great classes of fluids. If we put into a closed vessel a small quantity of a fluid of the first class, such as water, it will partly fill the vessel, and the rest of the vessel may either be empty or may contain a different fluid. Fluids having this property are called liquids. Water is a liquid, and if we put a little water into a bottle the water will lie at the bottom of the bottle, and will be separated by a distinct surface from the air or the vapour of water above it.

If, on the contrary, the fluid which we put into the closed vessel be one of the second class, then, however small a portion we introduce, it will expand and fill the vessel, or at least as much of it as is not occupied by a liquid.

Fluids having this property are called gases. Air is a gas, and if we first exhaust the air from a vessel and then introduce the smallest quantity of air, the air will immediately expand till it fills the whole vessel so that there is as much air in a cubic inch in one part of the vessel as in another.

Hence a gas cannot, like a liquid, be kept in an open-mouthed vessel.

The distinction, therefore, between a gas and a liquid is that, however large the space may be into which a portion of gas is introduced, the gas will expand and exert pressure on every part of its boundary, whereas a liquid will not expand more than a very small fraction of its bulk, even when the pressure is reduced to zero; and some liquids can even sustain a hydrostatic tension, or negative pressure, without their parts being separated.

The three principal states in which bodies are found are, therefore, the solid, the liquid, and the gaseous states.

Most substances are capable of existing in all these states, as, for instance, water exists in the forms of ice, water, and steam. A few solids, such as carbon, have not yet been melted; and a few gases, such as oxygen, hydrogen, and nitrogen, have not yet been liquefied or solidified, but these may be considered as exceptional cases, arising from the limited range of temperature and pressure which we can command in our experiments.

The ordinary effects of heat in modifying the physical state of bodies may be thus described. We may take water as a familiar example, and explain, when it is necessary, the different phenomena of other bodies.

At the lowest temperatures at which it has been observed water exists in the solid form as ice. When heat is communicated to very cold ice, or to any other solid body not at its melting temperature—

1.  The temperature rises.
2. The body generally expands (the only exception among solid bodies, as far as I am aware, is the iodide of silver, which has been found by M. Fizeau to contract as the temperature rises).
3. The rigidity of the body, or its resistance to change of form, generally diminishes. This phenomenon is more apparent in some bodies than in others. It is very conspicuous in iron, which when heated but not melted becomes soft and easily forged. The consistency of glass, resins, fats, and frozen oils alters very much with change of temperature. On the other hand, it is believed that steel wire is stiffer at 212°F. than at 32°F., and it has been shown by Joule and Thomson that the longitudinal elasticity of caoutchouc increases with the temperature between certain limits of temperature. When ice is very near its melting point it becomes very soft
4. A great many solid bodies are constantly in a state of evaporation or transformation into the gaseous state at their free surface. Camphor, iodine, and carbonate of ammonia are well-known examples of this. These solid bodies, if not kept in stoppered bottles, gradually disappear by evaporation, and the vapour which escapes from them may be recognised by its smell and by its chemical action. Ice, too, is continually passing into a state of vapour at its surface, and in a dry climate during a long frost large pieces of ice become smaller and at last disappear.

There are other solid bodies which do not seem to lose any of their substance in this way; at least, we cannot detect any loss. It is probable, however, that those solid bodies which can be detected by their smell are evaporating with extreme slowness. Thus iron and copper have each a well-known smell. This, however, may arise from chemical action at the surface, which sets free hydrogen or some other gas combined with a very small quantity of the metal.

FUSION

When the temperature of a solid body is raised to a sufficient height it begins to melt into a liquid. Suppose a small portion of the solid to be melted, and that no more heat is applied till the temperature of the remaining solid and of the liquid has become equalised; if a little more heat is then applied and the temperature again equalised there will be more liquid matter and less solid matter, but since the liquid and the solid are at the same temperature, that temperature must still be the melting temperature.

Hence, if the partly melted mass be kept well mixed together, so that the solid and fluid parts are at the same temperature, that temperature must be the melting temperature of the solid, and no rise of temperature will follow from the addition of heat till the whole of the solid has been converted into liquid.

The heat which is required to melt a certain quantity of a solid at the melting point into a liquid at the same temperature is called the latent heat of fusion.

It is called latent heat, because the application of this heat to the body does not raise its temperature or warm the body.

Those, therefore, who maintained heat to be a substance supposed that it existed in the fluid in a concealed or latent state, and in this way they distinguished it from the heat which, when applied to a body, makes it hotter, or raises the temperature. This they called sensible heat. A body, therefore, was said to possess so much heat. Part of this heat was called sensible heat, and to it was ascribed the temperature of the body. The other part was called latent heat, and to it was ascribed the liquid or gaseous form of the body.

The fact that a certain quantity of heat must be applied to a pound of melting ice to convert it into water is all that we mean in this treatise when we speak of this quantity of heat as the latent heat of fusion of a pound of water.

We make no assertion as to the state in which the heat exists in the water. We do not even assert that the heat communicated to the ice is still in existence as heat.

Besides the change from solid to liquid, there is generally a change of volume in the act of fusion. The water formed from the ice is of smaller, bulk than the ice, as is shown by ice floating in water, so that the total volume of the ice and water diminishes as the melting goes on.

On the other hand, many substances expand in the act of fusion, so that the solid parts sink in the fluid. During the fusion of the mass the volume in these cases increases.

It has been shown by Prof. J. Thomson,[note]Transactions of the Royal Society of Edinburgh, 1849.[/note] from the principles of the dynamical theory of heat, that if pressure is applied to a mixture of ice and water, it will not only compress both the ice and the water, but some of the ice will be melted at the same time, so that the total compression will be increased by the contraction of bulk due to this melting. The heat required to melt this ice being taken from the rest
of the mass, the temperature of the whole will diminish.

Hence the melting point is lowered by pressure in the case of ice. This deduction from theory was experimentally verified by Sir W. Thomson.

If the substance had been one of those which expand in melting, the effect of pressure would be to solidify some of the mixture, and to raise the temperature of fusion. Most of the substances of which the crust of the earth is composed expand in the act of melting. Hence their melting points will rise under great pressure. If the earth were throughout in a state of fusion, when the external parts began to solidify they would sink in the molten mass, and when they had sunk to a great depth they would remain solid under the enormous pressure even at a temperature greatly above the point of fusion of the same rock at the surface. It does not follow, therefore, that in the interior of the earth the matter is in a liquid state, even if the temperature is far above that of the fusion of rocks in our furnaces.

It has been shown by Sir W. Thomson that if the earth, as a whole, were not more rigid than a ball of glass of equal size, the attraction of the moon and sun would pull it out of shape, and raise tides on the surface, so that the solid earth would rise and fall as the sea does, only not quite so much. It is true that this motion would be so smooth and regular that we should not be able to perceive it in a direct way, but its effect would be to diminish the apparent rise of the tides of the ocean, so as to make them much smaller than they actually are.

It appears, therefore, from what we know of the tides of the ocean, that the earth as a whole is more rigid than glass, and therefore that no very large portion of its interior can be liquid. The effect of pressure on the melting point of bodies enables us to reconcile this conclusion with the observed increase of temperature as we descend in the earth’s crust, and the deductions as to the interior temperature founded on this fact by the aid of the theory of the conduction of heat.

 

EFFECT OF HEAT ON LIQUIDS.

When heat is applied to a liquid its effects are—

1. To warm the liquid. The quantity of heat required to raise the liquid one degree is generally greater than that required to raise the substance in the solid form one degree, and in general it requires more heat at high than at low temperatures to warm the liquid one degree.
2. To alter its volume. Most liquids expand as their temperature rises, but water contracts from 32°F. to 39°.1F., and then expands, slowly at first, but afterwards more rapidly.
3. To alter its physical state. Liquids, such as oil, tar, &c., which are sluggish in their motion, are said to be viscous. When they are heated their viscosity generally diminishes and they become more mobile. This is the case even with water, as appears by the experiments of M. O. E. Meyer.
When sulphur is heated, the melted sulphur undergoes several remarkable changes as its temperature rises, being mobile when first melted, then becoming remarkably viscous at a higher temperature, and again becoming mobile when still more heated. These changes are connected with chemical changes in the constitution of the sulphur, which are observed also in solid sulphur.
4. To convert the liquid into vapour.
Whatever be the temperature of a liquid which partially fills a vessel, it always gives off vapour till the remainder of the vessel is filled with vapour, and this goes on till the density of the vapour has reached a value which depends only on the temperature.

If in any way, as by the motion of a piston, the vessel be made larger, then more vapour will be formed till the density is the same as before. If the piston be pushed in, and the vessel made smaller, some of the vapour is condensed into the liquid state, but the density of the remainder of the vapour still remains the same.

If the remainder of the vessel, instead of containing nothing but the vapour of the liquid, contains any quantity of air or some other gas not capable of chemical action on the liquid, then exactly the same quantity of vapour will be formed, but the time required for the vapour to reach the further parts of the vessel will be greater, as it has to diffuse itself through the air in the vessel by a kind of percolation.

These laws of evaporation were discovered by Dalton.

The conversion of the liquid into vapour requires an amount of ‘latent heat’ which is generally much greater than the latent heat of fusion of the same substance.

In all substances, the density, pressure, and temperature are so connected that if we know any two of them the value of the third is determinate. Now in the case of vapours in contact with their own liquids or solids, there is for each temperature a corresponding density, which is the greatest density which the vapour can have at that temperature, without being condensed into the liquid or solid form.

Hence for each temperature there is also a maximum pressure which the vapour can exert.

A vapour which is at the maximum density and pressure corresponding to its temperature is called a saturated vapour. It is then just at the point of condensation, and the slightest increase of pressure or decrease of temperature will cause some of the vapour to be condensed. Professor Rankine[note]직지 주: William John Macquorn Rankine[/note] restricts the use of the word vapour by itself to the case of a saturated vapour, and when the vapour is not at the point of condensation he calls it superheated vapour, or simply gas.

 

BOILING.

When a liquid in an open vessel is heated to a temperature such that the pressure of its vapour at that temperature is greater than the pressure at a point in the interior of the liquid, the liquid will begin to evaporate at that point, so that a bubble of vapour will be formed there. This process, in which bubbles of vapour are formed in the interior of the liquid, is called boiling or ebullition.

When water is heated in the ordinary way by applying heat to the bottom of a vessel, the lowest layer of the water becomes hot first, and by its expansion it becomes lighter than the colder water above, and gradually rises, so that a gentle circulation of water is kept up, and the whole water is gradually warmed, though the lowest layer is always the hottest. As the temperature increases, the absorbed air, which is generally found in ordinary water, is expelled, and rises in small bubbles without noise. At last the water in contact with the heated metal becomes so hot that, in spite of the pressure of the atmosphere on the surface of the water, the additional pressure due to the water in the vessel, and the cohesion of the water itself, some of the water at the bottom is transformed into steam, forming a bubble adhering to the bottom of the vessel. As soon as a bubble is formed, evaporation goes on rapidly from the water all round it, so that it soon grows large, and rises from the bottom. If the upper part of the water into which the bubble rises is still below the boiling temperature, the bubble is condensed, and its sides come together with a sharp rattling noise, called simmering. But the rise of the bubbles stirs the water about much more vigorously than the mere expansion of the water, so that the water is soon heated throughout, and brought to the boil, and then the bubbles enlarge rapidly during their whole ascent, and burst into the air, throwwing the water about, and making the well-known softer and more rolling noise of boiling.

The steam, as it bursts out of the bubbles, is an invisible gas, but when it comes into the colder air it is cooled below its condensing point, and part of it is formed into a cloud consisting of small drops of water which float in the air. As the cloud of drops disperses itself and mixes with dry air the quantity of water in each cubic foot diminishes as the volume of any part of the cloud increases. The little drops of water begin to evaporate as soon as there is sufficient room for the vapour to be formed at the temperature of the atmosphere, and so the cloud vanishes again into thin air.

The temperature to which water must be heated before it boils depends, in the first place, on the pressure of the atmosphere, so that the greater the pressure, the higher the boiling temperature. But the temperature requires to be raised above that at which the pressure of steam is equal to that of the atmosphere, for the pressure of the vapour has to overcome not only the pressure due to the atmosphere and a certain depth of water, but that cohesion between the parts of the water of which the effects are visible in the tenacity of bubbles and drops. Hence it is possible to heat water 20°F. above its boiling point without ebullition. If a small quantity of metal-filings are now thrown into the water, the vapour by forming itself against the angular surface of these filings gets an advantage over the cohesion of the water, and produces a violent boiling, almost amounting to an explosion.

If a current of steam from a boiler is passed into a vessel of cold water, we have first the condensation of steam, accompanied with a very loud simmering noise, and a rapid heating of the water. When the water is sufficiently heated, the steam is not condensed, but escapes in bubbles, and the water is now boiling. If the boiler is at a high pressure, the steam from it will be at a temperature much above the boiling point in the open air, but in passing through the water in the open vessel it will cause some of it to evaporate, and when it issues from the water the temperature will be exactly that of the boiling point. For this reason, in finding the boiling point of a thermometer the instrument should not be allowed to dip in the water, but should be held in the steam.

As an instance of a different kind, let us suppose that the water is not pure, but contains some salt, such as common salt, or sulphate of soda, or any other substance which tends to combine with water, and from which the water must separate before it can evaporate. Water containing such substances in solution requires to be brought to a temperature higher than the boiling point of pure water before it will boil. Water, on the other hand, containing air or carbonic acid, will boil at a lower temperature than pure water till the gas is expelled.

If steam at 100°C. is passed into a vessel containing a strong solution of one of the salts we have mentioned, which has a tendency to combine with water, the condensation of the steam will be promoted by this tendency, and will go on even after the solution has been heated far above the ordinary boiling point, so that by passing steam at 100°C. into a strong solution of nitrate of soda, Mr. Peter Spence[note]Transactions of the British Association, 1869, p. 75.[/note] has heated it up to 121°I C.

The steam, however, which escapes, is still at 100°C.

If water at a temperature below 100°C. be placed in a vessel, and if by means of an air-pump we reduce the pressure of the air on the surface of the water, evaporation goes on and the surface of the water becomes colder than the interior parts. If we go on working the air-pump, the pressure is reduced to that of vapour of the temperature of the interior of the fluid. The water then begins to boil, exactly as in the ordinary way, and as it boils the temperature rapidly falls, the heat being expended in evaporating the water.

This experiment may be performed without an air-pump in the following way : Boil water in a flask over a gas-flame or spirit-lamp, and while it is boiling briskly cork the flask, and remove it from the flame. The boiling will soon cease, but if we now dash a little cold water over the flask, some of the steam in the upper part will be condensed, the pressure of the remainder will be diminished, and the water will begin to boil again. The experiment may be made more striking by plunging the flask entirely under cold water. The steam will be condensed as before, but the water, though it is cooled more rapidly than when the cold water was merely poured on the flask, retains its heat longer than the steam, and continues to boil for some time.

ON THE GASEOUS STATE.

The distinguishing property of gases is their power of
indefinite expansion. As the pressure is diminished the
volume of the gas not only increases, but before the pressure has been reduced to zero the volume of the gas has become greater than that of any vessel we can put it in.

This is the property without which a substance cannot be called a gas, but it is found that actual gases fulfil with greater or less degrees of accuracy certain numerical laws, which are commonly referred to as the ‘Gaseous Laws.’

LAW OF BOYLE

The first of these laws expresses the relation between the pressure and the density of a gas, the temperature being constant, and is usually stated thus : ‘The volume of a portion of gas varies inversely as the pressure.’

This law was discovered by Robert Boyle, and published by him in 1662, in an appendix to his ‘New Experiments, Physico-mechanical, &c., touching the Spring of the Air.’

Mariotte, about 1676, in his treatise ‘De la Nature de l’Air,’ enunciated the same law, and carefully verified it, and it is generally referred to by Continental writers as Mariotte’s law.

This law may also be stated thus :
The pressure of a gas is proportional to its density.

Another statement of the same law has been proposed by Professor Rankine, which I think places the law in a very clear light.

If we take a closed and exhausted vessel, and introduce into it one grain of air, this air will, as we know, exert a certain pressure on every square inch of the surface of the vessel. If we now introduce a second grain of air, then this second grain will exert exactly the same pressure on the sides of the vessel that it would have exerted if the first grain had not been there before it, so that the pressure will now be doubled. Hence we may state, as the property of a perfect gas, that any portion of it exerts the same pressure against the sides of a vessel as if the other portions had not been there.

Dalton extended this law to mixtures of gases of different kinds.

We have already seen that if several different portions of the same gas are placed together in a vessel, the pressure on any part of the sides of the vessel is the sum of the pressures which each portion would exert if placed by itself in the vessel.

Dalton’s law asserts that the same is true for portions of different gases placed in the same vessel, and that the pressure of the mixture is the sum of the pressures due to the several portions of gas, if introduced separately into the vessel and brought to the same temperature.

This law of Dalton is sometimes stated as if portions of gas of different kinds behave to each other in a different manner from portions of gas of the same kind, and we are told that when gases of different kinds are placed in the same vessel, each acts as if the other were a vacuum.

This statement, properly understood, is correct, but it seems to convey the impression that if the gases had been of the same kind some other result would have happened, whereas there is no difference between the two cases.

Another law established by Dalton is that the maximum density of a vapour in contact with its liquid is not affected by the presence of other gases. It has been shown by M. Regnault that when the vapour of the substance has a tendency to combine with the gas, the maximum density attainable by the vapour is somewhat increased.

Before the time of Dalton it was supposed that the cause of evaporation was the tendency of water to combine with air, and that the water was dissolved in the air just as salt is dissolved in water.

Dalton showed that the vapour of water is a gas, which just at the surface of the water has a certain maximum density, and which will gradually diffuse itself through the space above, whether filled with air or not, till, if the space is limited, the density of the vapour is a maximum throughout, or, if the space is large enough, till the water is all dried up.

The presence of air is so far from being essential to this process that the more air there is, the slower it goes on, because the vapour has to penetrate through the air by the slow process of diffusion.

The phenomenon discovered by Regnault that the density of vapour is slightly increased by the presence of a gas which has a tendency to combine with it, is the only instance in which there is any truth in the doctrine of a liquid being held in solution by a gas.

The law of Boyle is not perfectly fulfilled by any actual gas. It is very nearly fulfilled by those gases which we are not able to condense into liquids, and among other gases it is most nearly fulfilled when their temperature is much above their point of condensation.

When a gas is near its point of condensation its density increases more rapidly than the pressure. When it is actually at the point of condensation the slightest increase of pressure condenses the whole of it into a liquid, and in the liquid form the density increases very slowly with the pressure.

LAW OF CHARLES.

The second law of gases was discovered by Charles,[note]Professor of Physics at the Conservatoire des Arts et Metiers, Pans. Born 1746. Died 1823. Celebrated as having first employed hydrogen in balloons.[/note] but is commonly referred to as that of Gay-Lussac or of Dalton.[note]Dalton, in 1801, first published this law. Gay-Lussac published it, in 1802, independently of Dalton. In his memoir, however (Ann. tures for which it has hitherto been tested. de Chimie, xliii. p. 157 [1802]), he states that Citizen Charles had remarked, fifteen years before the date of his memoir, the equality of the dilatation of the principal gases; but, as Charles never published these results, he had become acquainted with them by mere chance.[/note] It may be stated thus:

The volume of a gas under constant pressure expands when raised from the freezing to the boiling temperature by the same fraction of itself, whatever be the nature of the gas.

It has been found by the careful experiments of M. Regnault, M. Rudberg, Prof. B. Stewart, and others that the volume of air at constant pressure expands from 1 to 1.3665 between 0°C. and 100°C. Hence 30 cubic inches of air at 0°C. would expand to about 41 cubic inches at 100°C.

If we admit the truth of Boyle’s law at all temperatures, and if the law of Charles is found to be true for a particular pressure, say that of the atmosphere, then it is easy to show that the law of Charles must be true for every other pressure. For if we call the volume v and the pressure p, then we may call the product of the numerical value of the volume and pressure v p, and Boyle’s law asserts that this product is constant, provided the temperature is constant. If then we are further informed that when p has a given value v is increased from 1 to 1.3665 when the temperature rises from the freezing point to the boiling point, the product v p will be increased in the same proportion at that particular pressure. But v p we know by Boyle’s law does not depend on the particular pressure, but remains the same for all pressures when the temperature remains the same. Hence, whatever be the pressure, the product v p will be increased in the proportion of 1 to 1.3665 when the temperature rises from 0°C. to 100°C.

The law of the equality of the dilatation of gases, which, as originally stated, applied only to the dilatation from 0°C. to 100°C., has been found to be true for all other temperatures for which it has hitherto been tested.

It appears, therefore, that gases are distinguished from other forms of matter, not only by their power of indefinite expansion so as to fill any vessel, however large, and by the great effect which heat has in dilating them, but by the uniformity and simplicity of the laws which regulate these changes. In the solid and liquid states the effect of a given change of pressure or of temperature in changing the volume of the body is different for every different substance. On the other hand, if we take equal volumes of any two gases, measured at the same temperature and pressure, their volumes will remain equal if we afterwards bring them both to any other temperature and pressure, and this although the two gases differ altogether in chemical nature and in density, provided they are both in the perfectly gaseous condition.

This is only one of many remarkable properties which point out the gaseous state of matter as that in which its physical properties are least complicated.

In our description of the physical properties of bodies as related to heat we have begun with solid bodies, as those which we can most easily handle, and have gone on to liquids, which we can keep in open vessels, and have now come to gases, which will escape from open vessels, and which are generally invisible. This is the order which is most natural in our first study of these different states. But as soon as we have been made familiar with the most prominent features of these different conditions of matter, the most scientific course of study is in the reverse order, beginning with gases, on account of the greater simplicity of their laws, then advancing to liquids, the more complex laws of which are much more imperfectly known, and concluding with the little that has been hitherto discovered about the constitution of solid bodies.

 

CHAPTER II. ON THERMOMETRY, OR THE THEORY OF TEMPERATURE.

Definition of Temperature.—The temperature of a body

is its thermal state considered with reference to its power of communicating heat to other bodies.

Definition of Higher and Lower Temperature.—If when two bodies are placed in thermal communication, one of the bodies loses heat, and the other gains heat, that body which gives out heat is said to have a higher temperature than that which receives heat from it.

Cor. If when two bodies are placed in thermal communication neither of them loses or gains heat, the two bodies are said to have equal temperatures or the same temperature. The two bodies are then said to be in thermal equilibrium. We have here a means of comparing the temperature of any two bodies, so as to determine which has the higher temperature, and a test of the equality of temperature which is independent of the nature of the bodies tested. But we have no means of estimating numerically the difference between two temperatures, so as to be able to assert that a certain temperature is exactly halfway between two other temperatures.

Law of Equal Temperatures.—Bodies whose temperatures are equal to that of the same body have themselves equal temperatures. This law is not a truism, but expresses the fact that if a piece of iron when plunged into a vessel of water is in thermal equilibrium with the water, and if the same piece of iron, without altering its temperature, is transferred to a vessel of oil, and is found to be also in thermal equilibrium with the oil, then if the oil and water were put into the same vessel they would themselves be in thermal equilibrium, and the same would be true of any other three substances.

This law, therefore, expresses much more than Euclid’s axiom that ‘Things which are equal to the same thing are equal to one another’, and is the foundation of the whole science of thermometry. For if we take a thermometer, such as we have already described, and bring it into intimate contact with different bodies, by plunging it into liquids, or inserting it into holes made in solid bodies, we find that the mercury in the tube rises or falls till it has reached a certain point at which it remains stationary. We then know that the thermometer is neither becoming hotter nor colder, but is in thermal equilibrium with the surrounding body. It follows from this, by the law of equal temperatures, that the temperature of the body is the same as that of the thermometer, and the temperature of the thermometer itself is known from the height at which the mercury stands in the tube.

Hence’the reading’ as it is called, of the thermometer— that is, the number of degrees indicated on the scale by the top of the mercury in the tube—informs us of the temperature of the surrounding substance, as well as of that of the mercury in the thermometer. In this way the thermometer may be used to compare the temperature of any two bodies at the same time or at different times, so as to ascertain whether the temperature of one of them is higher or lower than that of the other. We may compare in this way the temperatures of the air on different days; we may ascertain that water boils at a lower temperature at the top of a mountain than it does at the sea-shore, and that ice melts at the same temperature in all parts of the world.

For this purpose it would be necessary to carry the same thermometer to different places, and to preserve it with great care, for if it were destroyed and a new one made, we should have no certainty that the same temperature is indicated by the same reading in the two thermometers.

Thus the observations of temperature recorded during
sixteen years by Rinieri[note]Pupil of Galileo; died 1647.[/note] at Florence lost their scientific value after the suppression of the Accademia del Cimento, and the supposed destruction of the thermometers with which the observations were made. But when Antinori in 1829 discovered a number of the very thermometers used in the ancient observations, Libri[note]Annales de Chimie et de Physique, xlv. (1830).[/note] was able to compare them with Reaumur’s scale, and thus to show that the climate of Florence has not been rendered sensibly colder in winter by the clearing of the woods of the Apennines.

In the construction of artificial standards for the measurement of quantities of any kind it is desirable to have the means of comparing the standards together, either directly, or by means of some natural object or phenomenon which is easily accessible and not liable to change. Both methods are used in the preparation of thermometers.

We have already noticed two natural phenomena which take place at definite temperatures—the melting of ice and the boiling of water. The advantage of employing these temperatures to determine two points on the scale of the thermometer was pointed out by Sir Isaac Newton (‘Scala Graduum Caloris,’ Phil. Trans. 1701).

The first of these points of reference is commonly called the Freezing Point. To determine it, the thermometer is placed in a vessel filled with pounded ice or snow thoroughly moistened with water. If the atmospheric temperature be above the freezing point, the melting of the ice will ensure the presence of water in the vessel. As long as every part of the vessel contains a mixture of water and ice its temperature remains uniform, for if heat enters the vessel it can only melt some of the ice, and if heat escapes from the vessel some of the water will freeze, but the mixture can be made neither hotter nor colder till all the ice is melted or all the water frozen.

The thermometer is completely immersed in the mixture of ice and water for a sufficient time, so that the mercury has time to reach its stationary point. The position of the top of the mercury in the tube is then recorded by making a scratch on the glass tube. We shall call this mark the Freezing Point. It may be determined in this way with extreme accuracy, for, as we shall see afterwards, the temperature of melting ice is very nearly the same under very different pressures.

The other point of reference is called the Boiling Point. The temperature at which water boils depends on the pressure of the atmosphere. The greater the pressure of the air on the surface of the water, the higher is the temperature to which the water must be raised before it begins to boil.

To determine the Boiling Point, the stem of the thermometer is passed through a hole in the lid of a tall vessel, in the lower part of which water is made to boil briskly, so that the whole of the upper part, where the thermometer is placed, is filled with steam. When the thermometer has acquired the temperature of the current of steam the stem is drawn up through the hole in the lid of the vessel till the top of the column of mercury becomes visible. A scratch is then made on the tube to indicate the boiling point.

In careful determinations of the boiling point no part of the thermometer is allowed to dip into the boiling water, because it has been found by Gay-Lussac that the temperature of the water is not always the same, but that it boils at different temperatures in different kinds of vessels. It has been shown, however, by Rudberg that the temperature of the steam which escapes from boiling water is the same in every kind of vessel, and depends only on the pressure at the surface of the water. Hence the thermometer is not dipped in the water, but suspended in the issuing steam. To ensure that the temperature of the steam shall be the same when it reaches the thermometer as when it issues from the boiling water, the sides of the vessel are sometimes protected by what is called a steam-jacket. A current of steam is made to play over the outside of the sides of the vessel. The vessel is thus raised to the same temperature as the steam itself, so that the steam cannot be cooled during its passage from the boiling water to the thermometer.

For instance, if we take any tall narrow vessel, as a coffee-pot, and cover its mouth and part of its side with a wider vessel turned upside down, taking care that there shall be plenty of room for the steam to escape, then if we boil a small quantity of water in the coffee-pot, a thermometer placed in the steam above will be raised to the exact temperature of the boiling point of water corresponding to the state of the barometer at the time.

To mark the level of the mercury on the tube of the thermometer without cooling it, we must draw it up through a cork or a plug of india-rubber in the steam-jacket through which the steam passes till we can just see the top of the column of mercury. A mark must then be scratched on the glass to register the boiling point. This experiment of exposing a thermometer to the steam of boiling water is an important one, for it not only supplies a means of graduating thermometers, and testing them when they have been graduated, but, since the temperature at which water boils depends on the pressure of the air, we may determine the pressure of the air by boiling water when we are not able to measure it by means of the appropriate instrument, the barometer.

We have now obtained two points of reference marked by scratches on the tube of the thermometer—the freezing point and the boiling point. We shall suppose for the present that when the boiling point was marked the barometer happened to indicate the standard pressure of 29.905 inches of mercury at 32°F. at the level of the sea in the latitude of London. In this case the boiling point is the standard boiling point. In any other case it must be corrected.

Our thermometer will now agree with any other properly constructed thermometer at these two temperatures.

In order to indicate other temperatures, we must construct a scale—that is, a series of marks—either on the tube itself or on a convenient part of the apparatus close to the tube and well fastened to it.

For this purpose, having settled what values we are to give to the freezing and the boiling points, we divide the space between those points into as many equal parts as there are degrees between them, and continue the series of equal divisions up and down the scale as far as the tube of the thermometer extends.

Three different ways of doing this are still in use, and, as we often find temperatures stated according to a different scale from that which we adopt ourselves, it is necessary to know the principles on which these scales are formed.

The Centigrade scale was introduced by Celsius.[note]Professor of Astronomy in the University of Upsala.[/note] In it the freezing point is marked 0° and called zero, and the boiling point is marked 100°.

The obvious simplicity of this mode of dividing the space between the points of reference into 100 equal parts and calling each of these a degree, and reckoning all temperatures in degrees from the freezing point, caused it to be very generally adopted, along with the French decimal system of measurement, by scientific men, especially on the Continent of Europe. It is true that the advantage of the decimal system is not so great in the measurement of temperatures as in other cases, as it merely makes it easier to remember the freezing and boiling temperatures, but the graduation is not too fine for the roughest purposes, while for accurate measurements the degrees may be subdivided into tenths and hundredths.

The other two scales are called by the names of those who introduced them.

Fahrenheit, of Dantzig, about 1714, first constructed thermometers comparable with each other. In Fahrenheit’s scale the freezing point is marked 32°, and the boiling point 212°, the space between being divided into 180 equal parts, and the graduation extended above and below the points of reference. A point 32 degrees below the freezing point is called zero, or 0°, and temperatures below this are indicated by the number of degrees below zero.

This scale is very generally used in English-speaking countries for purposes of ordinary life, and also for those of science, though the Centigrade scale is coming into use among those who wish their results to be readily followed by foreigners.

The only advantages which can be ascribed to Fahrenheit’s scale, besides its early introduction, its general diffusion, and its actual employment by so many of our countrymen, are that mercury expands almost exactly one ten-thousandth of its volume at 142°F. for every degree of Fahrenheit’s scale, and that the coldest temperature which we can get by mixing snow and salt is near the zero of Fahrenheit’s scale.

To compare temperatures given in Fahrenheit’s scale with temperatures given in the Centigrade scale we have only to remember that 0° Centigrade is 32° Fahrenheit, and that five degrees Centigrade are equal to nine of Fahrenheit.[note]직지 주: F=9/5 C + 32[/note]

The third thermometric scale is that of Réaumur. In this scale the freezing point is marked 0° and the boiling point 80°. I am not aware of any advantage of this scale. It is used to some extent on the Continent of Europe for medical and domestic purposes. Four degrees of Réaumur correspond to five Centigrade and to nine of Fahrenheit.

The existence of these three thermometric scales furnishes an example of the inconvenience of the want of uniformity in systems of measurement. The whole of what we have said about the comparison of the different scales might have been omitted if any one of these scales had been adopted by all who use thermometers. Instead of spending our time in describing the arbitrary proposals of different men, we should have gone on to investigate the laws of heat and the properties of bodies.

We shall afterwards have occasion to use a scale differing in its zero-point from any of those we have considered, but when we do so we shall bring forward reasons for its adoption depending on the nature of things and not on the predilections of men.

If two thermometers are constructed of the same kind of glass, with tubes of uniform bore, and are filled with the same liquid and then graduated in the same way, they may be considered for ordinary purposes as comparable instruments; so that though they may never have been actually compared together, yet in ascertaining the temperature of anything there will be very little difference whether we use the one thermometer or the other.

But if we desire great accuracy in the measurement of temperature, so that the observations made by different observers with different instruments may be strictly comparable, the only satisfactory method is by agreeing to choose one thermometer as a standard and comparing all the others with it.

All thermometers ought to be made with tubes of as uniform bore as can be found; but for a standard thermometer the bore should be calibrated—that is to say, its size should be measured at short intervals all along its length.

For this purpose, before the bulb is blown, a small quantity of mercury is introduced into the tube and moved along the tube by forcing air into the tube behind it. This is done by squeezing the air out of a small india-rubber ball which is fastened to the end of the tube.

If the length of the column of mercury remains exactly the same as it passes along the tube, the bore of the tube must be uniform ; but even in the best tubes there is always some want of uniformity.

But if we introduce a short column of mercury into the tube, then mark both ends of the column, and move it on its own length, till one end comes exactly to the mark where the other end was originally, then mark the other end, and move it on again, we shall have a series of marks on the tube such that the capacity of the tube between any two consecutive marks will be the same, being equal to that of the column of mercury.

By this method, which was invented by Gay-Lussac, a number of divisions may be marked on the tube, each of which contains the same volume, and though they will probably not correspond to degrees when the tube is made up into a thermometer, it will be easy to convert the reading of this instrument into degrees by multiplying it by a proper factor, and in the use of a standard instrument this trouble is readily undertaken for the sake of accuracy.

The tube having been prepared in this way, one end is heated till it is melted, and it is blown into a bulb by forcing air in at the other end of the tube. In order to avoid introducing moisture into the tube, this is done, not by the mouth, but by means of a hollow india-rubber ball, which is fastened to the end of the tube.

The tube of a thermometer is generally so narrow that mercury will not enter it, for a reason which we shall explain when we come to the properties of liquids. Hence the following method is adopted to fill the thermometer. By rolling paper round the open end of the tube, and making the tube thus formed project a little beyond the glass tube, a cavity is formed, into which a little mercury is poured. The mercury, however, will not run down the tube of the thermometer, partly because the bulb and tube are already full of air, and partly because the mercury requires a certain pressure from without to enter so narrow a tube. The bulb is therefore gently heated so as to cause the air to expand, and some of the air escapes through the mercury. When the bulb cools, the pressure of the air in the bulb becomes less than the pressure of the air outside, and the difference of these pressures is sufficient to make the mercury enter the tube, when it runs down and partially fills the bulb.

In order to get rid of the remainder of the air, and of any moisture in the thermometer, the bulb is gradually heated till the mercury boils. The air and steam escape along with the vapour of mercury, and as the boiling continues the last remains of air are expelled through the mercury at the top of the tube. When the boiling ceases, the mercury runs back into the tube, which is thus perfectly filled with mercury.

While the thermometer is still hotter than any temperature at which it will afterwards be used, and while the mercury or its vapour completely fills it, a blowpipe flame is made to play on the top of the tube, so as to melt it and close the end of the tube. The tube, thus closed with its own substance, is said to be ‘hermetically sealed.'[note]’ From Hermes or Mercury, the imagined inventor of chemistry.’—Johnson’s Dict.[/note]

There is now nothing in the tube but mercury, and when the mercury contracts so as to leave a space above it, this space is either empty of all gross matter, or contains only the vapour of mercury. If, in spite of all our precautions, there is still some air in the tube, this can easily be ascertained by inverting the thermometer and letting some of the mercury glide towards the end of the tube. If the instrument is perfect, it will reach the end of the tube and completely fill it. If there is air in the tube the air will form an elastic cushion, which will prevent the mercury from reaching the end of the tube, and will be seen in the form of a small bubble.

We have next to determine the freezing and boiling points, as has been already described, but certain precautions have still to be observed. In the first place, glass is a substance in which internal changes go on for some time after it has been strongly heated, or exposed to intense forces. In fact, glass is in some degree a plastic body. It is found that after a thermometer has been filled and sealed the capacity of the bulb diminishes slightly, and that this change is comparatively rapid at first, and only gradually becomes insensible as the bulb approaches its ultimate condition. It causes the freezing point to rise in the tube to 0°.3 or 0°.5, and if, after the displacement of the zero, the mercury be again boiled, the zero returns to its old place and gradually rises again.

This change of the zero-point was discovered by M. Flaugergues.[note]Ann. de Chimie et de Physique, xxi. p. 333 (1822).[/note] It may be considered complete in from four to six months.[note]Dr. Joule, however, finds that the rise of the freezing point of a delicate thermometer has been going on for twenty-six years, though the changes are now exceedingly minute.—Phil. Soc. Manchester, Feb. 22, 1870.[/note] In order to avoid the error which it would introduce into the scale, the instrument should, if possible, have its zero determined some months after it has been filled, and since even the determination of the boiling point of water produces a slight depression of the freezing point (that is, an expansion of the bulb), the freezing point should not be determined after the boiling point, but rather before it.

When the boiling point is determined, the barometer is probably not at the standard height. The mark made on the thermometer must, in graduating it, be considered to represent, not the standard boiling point, but the boiling point corresponding to the observed height of the barometer, which may be found from the tables.

To construct a thermometer in this elaborate way is by no means an easy task, and even when two thermometers have been constructed with the utmost care, their readings at points distant from the freezing and boiling points may not agree, on account of differences in the law of expansion of the glass of the two thermometers. These differences, however, are small, for all thermometers are made of the same description of glass.

But since the main object of thermometry is that all thermometers shall be strictly comparable, and since thermometers are easily carried from one place to another, the best method of obtaining this object is by comparing all thermometers either directly or indirecdy with a single standard thermometer. For this purpose, the thermometers, after being properly graduated, are all placed along with the standard thermometer in a vessel, the temperature of which can be maintained uniform for a considerable time. Each thermometer is then compared with the standard thermometer.

A table of corrections is made for each thermometer by entering the reading of that thermometer, along with the correction which must be applied to that reading to reduce it to the reading of the standard thermometer. This is called the proper correction for that reading. If it is positive it must be added to the reading, and if negative it must be subtracted from it.

By bringing the vessel to various temperatures, the corrections at these temperatures for each thermometer are ascertained, and the series of corrections belonging to each thermometer is made out and preserved along with that thermometer.

Any thermometer may be sent to the Observatory at Kew, and will be returned with a list of corrections, by the application of which, observations made with that thermometer become strictly comparable with those made by the standard thermometer at Kew, or with any other thermometer similarly corrected. The charge for making the comparison is very small compared with the expense of making an original standard thermometer, and the scientific value of observations made with a thermometer thus compared is greater than that of observations made with the most elaborately prepared thermometer which has not been compared with some existing and known standard instrument.

I have described at considerable length the processes by which the thermometric scale is constructed, and those by which copies of it are multiplied, because the practical establishment of such a scale is an admirable instance of the method by which we must proceed in the scientific observation of a phenomenon such as temperature, which, for the present, we regard rather as a quality, capable of greater or less intensity, than as a quantity which may be added to or subtracted from other quantities of the same kind.

A temperature, so far as we have yet gone in the science of heat, is not considered as capable of being added to another temperature so as to form a temperature which is the sum of its components. When we are able to attach a distinct meaning to such an operation, and determine its result, our conception of temperature will be raised to the rank of a quantity. For the present, however, we must be content to regard temperature as a quality of bodies, and be satisfied to know that the temperatures of all bodies can be referred to their proper places in the same scale.

For instance, we have a right to say that the temperatures of freezing and boiling differ by 180° Fahrenheit; but we have as yet no right to say that this difference is the same as that between the temperatures 300° and 480° on the same scale. Still less can we assert that a temperature of
244°F. = 32°+ 212°
is equal to the sum of the temperatures of freezing and boiling. In the same way, if we had nothing by which to measure time except the succession of our own thoughts, we might be able to refer each event within our own experience to its proper chronological place in a series, but we should have no means of comparing the interval of time between one pair of events with that between another pair, unless it happened that one of these pairs was included within the other pair, in which case the interval between the first pair must be the smallest. It is only by observation of the uniform or periodic motions of bodies, and by ascertaining the conditions under which certain motions are always accomplished in the same time, that we have been enabled to measure time, first by days and years, as indicated by the heavenly motions, and then by hours, minutes, and seconds, as indicated by the pendulums of our clocks, till we are now able, not only to calculate the time of vibration of different kinds of light, but to compare the time of vibration of a molecule of hydrogen set in motion by an electric discharge through a glass tube, with the time of vibration of another molecule of hydrogen in the sun, forming part of some great eruption of rosy clouds, and with the time of vibration of another molecule in Sirius which has not transmitted its vibrations to our earth, but has simply prevented vibrations arising in the body of that star from reaching us.

In a subsequent chapter we shall consider the further progress of our knowledge of Temperature as a Quantity.

ON THE AIR THERMOMETER.

The original thermometer invented by Galileo was an air thermometer. It consisted of a glass bulb with a long neck. The air in the bulb was heated, and then the neck was plunged into a coloured liquid. As the air in the bulb cooled, the liquid rose in the neck, and the higher the liquid the lower the temperature of the air in the bulb. By putting the bulb into the mouth of a patient, and noting the point to which the liquid was driven down in the tube, a physician might estimate whether the ailment was of the nature of a fever or not. Such a thermometer has several obvious merits. It is easily constructed, and gives larger indications for the same change of temperature than a thermometer containing any liquid as the thermometric substance. Besides this, the air requires less heat to warm it than an equal bulk of any liquid, so that the air thermometer is very rapid in its indications. The great inconvenience of the instrument as a means of measuring temperature is, that the height of the liquid in the tube depends on the pressure of the atmosphere as well as on the temperature of the air in the bulb. The air thermometer cannot therefore of itself tell us anything about temperature. We must consult the barometer at the same time, in order to correct the reading of the air thermometer. Hence the air thermometer, to be of any scientific value, must be used along with the barometer, and its readings are of no use till after a process of calculation has been gone through. This puts it at a great disadvantage compared with the mercurial thermometer as a means of ascertaining temperatures. But if the researches on which we are engaged are of so important a nature that we are willing to undergo the labour of double observations and numerous calculations, then the advantages of the air thermometer may again preponderate.

We have seen that in fixing a scale of temperature after marking on our thermometer two temperatures of reference and filling up the interval with equal divisions, two thermometers containing different liquids will not in general agree except at the temperatures of reference.

If, on the other hand, we could secure a constant pressure in the air thermometer, then if we exchange the air for any other gas, all the readings will be exactly the same provided the reading at one of the temperatures of reference is the same. It appears, therefore, that the scale of temperatures as indicated by an air thennometer has this advantage over the scale indicated by mercury or any other liquid or solid, that whereas no two liquid or solid substances can be made to agree in their expansion throughout the scale, all the gases agree with one another. In the absence of any better reasons for choosing a scale, the agreement of so many substances is a reason why the scale of temperatures furnished by the expansion of gases should be considered as of great scientific value. In the course of our study we shall find that there are scientific reasons of a much higher order which enable us to fix on a scale of temperature, based not on a probability of this kind, but on a more intimate knowledge of the properties of heat. This scale, so far as it has been investigated, is found to agree very closely with that of the air thermometer.

There is another reason, of a practical kind, in favour of the use of air as a thermometric substance, namely, that air remains in the gaseous state at the lowest as well as the highest temperatures which we can produce, and there are no indications in either case of its approaching to a change of state. Hence air, or one of the permanent gases, is of the greatest use in estimating temperatures lying far outside of the temperatures of reference, such, for instance, as the freezing point of mercury or the melting point of silver.

We shall consider the practical method of using air as a thermometric substance when we come to Gasometry. In the meantime let us consider the air thermometer in its simplest form, that of a long tube of uniform bore closed at one end, and containing air or some other gas which is separated from the outer air by a short column of mercury, oil, or some other liquid which is capable of moving freely along the tube, while at the same time it prevents all communication between the confined air and the atmosphere. We shall also suppose that the pressure acting on the confined air is in some way maintained constant during the course of the experiments we are going to describe.

The air thermometer is first surrounded with ice and ice-cold water. Let us suppose that the upper surface of the air marked ‘Freezing.’ The thermometer is then surrounded with the steam rising from water boiling under an atmospheric pressure of 29.905 inches of mercury. Let the surface of the enclosed air now stand at the point marked ‘Boiling.’ In this way, the two temperatures of reference are to be marked on the tube.

To complete the scale of the thermometer we must divide the distance between boiling and freezing into a selected number of equal parts, and carry this graduation up and down the tube beyond the freezing and boiling points with degrees of the same length.

Of course, if we carry the graduation far enough down the tube, we shall at last come to the bottom of the tube. What will be the reading at that point? and what is meant by it?

To determine the reading at the bottom of the tube is a very simple matter. We know that the distance of the freezing point from the bottom of the tube is to the distance of the boiling point from the bottom in the proportion of 1 to 1.3665, since this is the dilatation of air between the freezing and the boiling temperatures. Hence it follows, by an easy arithmetical calculation, that if, as in Fahrenheit’s scale, the freezing point is marked 32°, and the boiling point 212°, the bottom of the tube must be marked —459°.13′. If, as in the Centigrade scale, the freezing point is marked 0°, and the boiling point 100°, the bottom of the tube will be marked —272°.85. This, then, is the reading at the bottom of the scale.

The other question, What is meant by this reading? requires a more careful consideration. We have begun by defining the measure of the temperature as the reading of the scale of our thermometer when it is exposed to that temperature. Now if the reading could be observed at the bottom of the tube, it would imply that the volume of the air had been reduced to nothing. It is hardly necessary to say that we have no expectation of ever observing such a reading. If it were possible to abstract from a substance all the heat it contains, it would probably still remain an extended substance, and would occupy a certain volume. Such an abstraction of all its heat from a body has never been effected, so that we know nothing about the temperature which would be indicated by an air thermometer placed in contact with a body absolutely devoid of heat. This much we are sure of, however, that the reading would be above —459°.13F.

It is exceedingly convenient, especially in dealing with questions relating to gases, to reckon temperatures, not from the freezing point, or from Fahrenheit’s zero, but from the bottom of the tube of the air thermometer.

This point is then called the absolute zero of the air thermometer, and temperatures reckoned from it are called absolute temperatures. It is probable that the dilatation of a perfect gas is a little less than 1.3665. If we suppose it 1.366, then absolute zero will be —460° on Fahrenheit’s scale, or —273°[latex]\frac{1}{3}[/latex] Centigrade.

If we add 460° to the ordinary reading on Fahrenheit’s scale, we shall obtain the absolute temperature in Fahrenheit’s degrees.

If we add 273°[latex]\frac{1}{3}[/latex] to the Centigrade reading, we shall obtain the absolute temperature in Centigrade degrees.

We shall often have occasion to speak of absolute temperature by the air thermometer. When we do so we mean nothing more than what we have just said—namely, temperature reckoned from the bottom of the tube of the air thermometer. We assert nothing as to the state of a body deprived of all its heat, about which we have no experimental knowledge.

One of the most important applications of the conception of absolute temperature is to simplify the expression of the two laws discovered respectively by Boyle and by Charles. The laws may be combined into the statement that the product of the volume and pressure of any gas is proportional to the absolute temperature.

For instance, if we have to measure quantities of a gas by their volumes under various conditions as to temperature and pressure, we can reduce these volumes to what they would be at some standard temperature and pressure.

Thus if V, P, T be the actual volume, pressure, and absolute temperature, and V0 the volume at the standard pressure P0, and the standard temperature T0, then

[latex]\farc{V P}{T} = \frac{V_0 P_0}{T_0}[/latex]

or

[latex]V_0 = V \frac{P}{P_0}\frac{T_0}{T}[/latex]

If we have only to compare the relative quantities of the gas in different measurements in the same series of experiments, we may suppose P0 and T0 both unity, and use the quantity [latex]\frac{V P}{T}[/latex] without always multiplying it by [latex]\frac{T_0}{P_0}[/latex], which is a constant quantity.[note]For a full account of the methods of measuring gases the student is referred to Bunsen’s Gasometry, translated by Roscoe.[/note]

The great scientific importance of the scale of temperature as determined by means of the air or gas thermometer arises from the fact, established by the experiments of Joule and Thomson, that the scale of temperature derived from the expansion of the more permanent gases is almost exactly the same as that founded upon purely thermodynamic considerations, which are independent of the peculiar properties of the thermometric body. This agreement has been experimentally verified only within a range of temperature between 0°C. and 100°C. If, however, we accept the molecular theory of gases, the volume of a perfect gas ought to be exactly proportional to the absolute temperature on the thermodynamic scale, and it is probable that as the temperature rises the properties of real gases approximate to those of the theoretically perfect gas.

All the thermometers which we have considered have been constructed on the principle of measuring the expansion of a substance as the temperature rises. In certain cases it is convenient to estimate the temperature of a substance by the heat which it gives out as it cools to a standard temperature. Thus if a piece of platinum heated in a furnace is dropped into water, we may form an estimate of the temperature of the furnace by the amount of heat communicated to the water. Some have supposed that this method of estimating temperatures is more scientific than that founded on expansion. It would be so if the same quantity of heat always caused the same rise of temperature, whatever the original temperature of the body. But the specific heat of most substances increases as the temperature rises, and it increases in different degrees for different substances, so that this method cannot furnish an absolute scale of temperature. It is only in the case of gases that the specific heat of a given mass of the substance remains the same at all temperatures.

There are two methods of estimating temperature which are founded on the electrical properties of bodies. We cannot, within the limits of this treatise, enter into the theory of these methods, but must refer the student to works on electricity. One of these methods depends on the fact that in a conducting circuit formed of two different metals, if one of the junctions be warmer than the other, there will be an electromotive force which will produce a current of electricity in the circuit, and this may be measured by means of a galvanometer. In this way very minute differences of temperature between the ends of a piece of metal may be detected. Thus if a piece of iron wire is soldered at both ends to a copper wire, and if one of the junctions is at a place where we cannot introduce an ordinary thermometer, we may ascertain its temperature by placing the other junction in a vessel of water and adjusting the temperature of the water till no current passes. The temperature of the water will then be equal to that of the inaccessible junction.

Electric currents excited by differences of temperature in different parts of a metallic circuit are callcd thermo-electric currents. An arrangement by which the electromotive forces arising from a number of junctions may be added together is called a thermopile[note]직지 주: a set of thermocouples arranged for measuring small quantities of radiant heat. – 열전퇴(熱電堆), 열전대열(熟電對列)[/note], and is used in experiments on the heating effect of radiation, because it is more sensitive to changes of temperature caused by small quantities of heat than any other instrument

Professor Tait[note]Proceedings of the Royal Society of Edinburgh, 1870-71.[/note] has found that if [latex]t_1[/latex], and [latex]t_2[/latex] denote the temperatures of the hot and cold junction of two metals, the electromotive force of the circuit formed by these two
metals is

[latex]A(t_1 – t_2)[T – \frac{1}{2}(t_1 + t_2)],[/latex]

where [latex]A[/latex] is a constant depending on the nature of the metals, and [latex]T[/latex] is a temperature also depending on the metals, such that when one junction is as much hotter than [latex]T[/latex] as the other is colder, no current is produced, [latex]T[/latex] may be called the neutral temperature for the two metals. For copper and iron it is about 284°C.

The other method of estimating the temperature of a place at which we cannot set a thermometer is founded on the increase of the electric resistance of metals as the temperature rises. This method has been successfully employed by Mr. Siemens.[note]Proceedings of the Royal Socicty, April 27, 1871.[/note] Two coils of the same kind of fine platinum wire are prepared so as to have equal resistance. Their ends are connected with long thick copper wires, so that the coils may be placed if necessary a long way from the galvanometer. These copper terminals are also adjusted so as to be of the same resistance for both coils. The resistance of the terminals should be small as compared with that of the coils. One of the coils is then sunk, say to the bottom of the sea, and the other is placed in a vessel of water, the temperature of which is adjusted till the resistance of both coils is the same. By ascertaining with a thermometer the temperature of the vessel of water, that of the bottom of the sea may be deduced.

Mr. Siemens has found that the resistance of the metals may be expressed by a formula of the form

[latex]R = \alpha \sqrt{T} + \beta T + \gamma,[/latex]

where [latex]R[/latex] is the resistance, [latex]T[/latex] the absolute temperature, and a ft [latex]\alpha \enspace \beta \enspace \gamma[/latex] coefficients. Of these [latex]\alpha[/latex] is the largest, and the resistance depending on it increases as the square root of the absolute temperature, so that the resistance increases more slowly as the temperature rises. The second term, [latex]\beta T[/latex], is proportional to the temperature and may be attributed to the expansion of the substance. The third term is constant.